Ha habido diversos modelos de pandemias [3,2] propuestos como sistemas de transición [4]. Presentamos aquí un modelo alternativo propio, inspirado en aquellos pero con características propias: Consideramos tanto transiciones en los modelos clásicos del tipo SIR como las gráficas de contacto y de contagio.
Sea 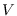 el conjunto de individuos en una localidad donde se desarrolla una epidemia. En todo momento, se tiene una partición de
el conjunto de individuos en una localidad donde se desarrolla una epidemia. En todo momento, se tiene una partición de 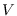 en las clases siguientes:
en las clases siguientes:
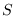 : la clase de susceptibles, individuos que pueden contagiarse,
: la clase de susceptibles, individuos que pueden contagiarse,
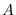 : la clase de asintomáticos, individuos que se han contagiado pero no presentan síntomas,
: la clase de asintomáticos, individuos que se han contagiado pero no presentan síntomas,
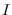 : la clase de infecciosos, individuos que se han contagiado y están enfermos,
: la clase de infecciosos, individuos que se han contagiado y están enfermos,
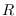 : la clase de recuperados, individuos que habiendo sido contagiados, superan el contagio y sanan, y
: la clase de recuperados, individuos que habiendo sido contagiados, superan el contagio y sanan, y
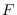 : la clase de fallecidos, individuos que han muerto por la enfermedad.
: la clase de fallecidos, individuos que han muerto por la enfermedad.
Consideramos inicialmente una gráfica (no-dirigida) de contactos,
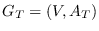 donde los nodos son los individuos y
donde los nodos son los individuos y
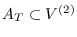 consta de las aristas consistentes de parejas de individuos con cercanía geográfica, familiares o de trabajo. La distancia entre dos nodos es el número de aristas de las que consta el camino más corto que los une en la gráfica, adirigida,
consta de las aristas consistentes de parejas de individuos con cercanía geográfica, familiares o de trabajo. La distancia entre dos nodos es el número de aristas de las que consta el camino más corto que los une en la gráfica, adirigida, 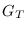 .
Para cada
.
Para cada 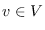 sea
sea
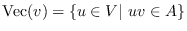 la vecindad de
la vecindad de 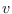 en esa gráfica de contactos, es decir un nodo
en esa gráfica de contactos, es decir un nodo 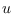 es vecino de
es vecino de 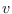 si está a distancia 1 de
si está a distancia 1 de 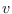 .
.
Sea
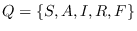 el conjunto de estados que puede asumir cada nodo, o de clases en la que están los nodos.
En cada momento
el conjunto de estados que puede asumir cada nodo, o de clases en la que están los nodos.
En cada momento 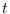 se tiene una función de asignación:
se tiene una función de asignación:
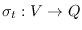 que a cada nodo le asocia un estado en el tiempo
que a cada nodo le asocia un estado en el tiempo 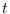 . Se dice que el individuo
. Se dice que el individuo 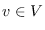 “es”
“es” 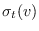 al momento
al momento 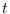 .
.
Se le da a la gráfica una estructura de transición probabilista. Para cada momento 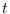 , cada nodo
, cada nodo 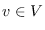 , para todos
, para todos 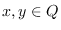 sea
sea
La correspondiente matriz de transición es
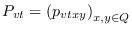 .
Las entradas de la matriz de transición se evalúan como sigue:
Se tiene pues la matriz de transición de la forma
.
Las entradas de la matriz de transición se evalúan como sigue:
Se tiene pues la matriz de transición de la forma
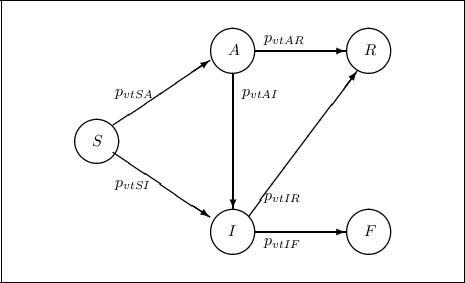
Figure:
Diagrama de transición entre estados.
 |
Ya que 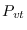 es una matriz triangular superior, sus valores propios son los que aparecen en la diagonal. En tanto que las probabilidades de transición efectiva, las mostradas en la Figura 2, sean pequeñas, los valores propios de
es una matriz triangular superior, sus valores propios son los que aparecen en la diagonal. En tanto que las probabilidades de transición efectiva, las mostradas en la Figura 2, sean pequeñas, los valores propios de 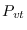 serán más cercanos a 1, lo que denota una situación de equilibrio o estable. Conforme crecen las probabilidades de transición efectiva, cada individuo habrá de padecer la epidemia para finalizar, ya sea sano o fallecido.
serán más cercanos a 1, lo que denota una situación de equilibrio o estable. Conforme crecen las probabilidades de transición efectiva, cada individuo habrá de padecer la epidemia para finalizar, ya sea sano o fallecido.
El diagrama de transición correspondiente a la matriz 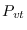 se muestra en la Figura 2. Las probabilidades en la diagonal son las de quedarse en un mismo estado. Para todos
se muestra en la Figura 2. Las probabilidades en la diagonal son las de quedarse en un mismo estado. Para todos 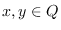 denotemos por
denotemos por
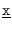 a la transición que va de
a la transición que va de 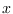 a
a 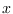 mismo y por
mismo y por
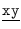 a la que va del estado
a la que va del estado 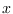 al
al 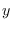 . Así, toda ruta para ir de
. Así, toda ruta para ir de 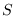 a cualquiera de los estados finales se expresa mediante la expresión regular
a cualquiera de los estados finales se expresa mediante la expresión regular
En particular, se puede distinguir las clases siguientes de trayectorias:
- De susceptible a fallecido:
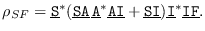
- De asintomático a recuperado:
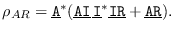
- De asintomático a fallecido:
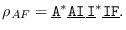
- De infeccioso a recuperado:
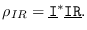
- De infeccioso a fallecido:
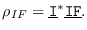
Cada transición de un estado a otro, o si se quiere, cada expresión regular, determina una probabilidad. Así por ejemplo
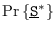 es la probabilidad de que un individuo no padezca de ningún contagio, la condición
es la probabilidad de que un individuo no padezca de ningún contagio, la condición
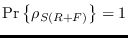 indica que todos los individuos han de pasar por la epidemia, finalizando cada uno como recuperado o fallecido, y la condición
indica que todos los individuos han de pasar por la epidemia, finalizando cada uno como recuperado o fallecido, y la condición
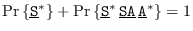 indica que la epidemia no tiene infecciosos pero sí se mantiene en estado latente: hay individuos contagiados pero asintomáticos.
indica que la epidemia no tiene infecciosos pero sí se mantiene en estado latente: hay individuos contagiados pero asintomáticos.
Para ilustrar el cálculo de probabilidades, vemos que la probabilidad de recorrer una trayectoria del tipo
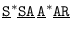 es
es
![\begin{displaymath}
p=\left[\prod_{\kappa=0}^{\iota-1}p_{v,t+\kappa,SS}\right]p_...
...bda-1}p_{v,t+\iota+\kappa,AA}\right]p_{v,t+\iota+\lambda,AR}.
\end{displaymath}](img260.png) |
(34) |
Suponiendo que las probabilidades involucradas en (34) se mantuvieran constantes en el transcurso de la ruta:
y en este caso, la probabilidad de arribar al estado 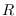 según
según
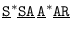 es
es
De manera similar se calcula la probabilidad de arribar desde cualquiera de los estados de asintomáticos o infecciosos a uno terminal, ya sea de recuperación o de fallecimiento.
Sea pues 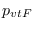 la probabilidad de arribar desde
la probabilidad de arribar desde 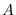 o
o 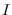 a
a 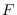 y sea
y sea 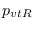 la de arribar desde
la de arribar desde 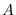 o
o 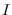 a
a 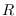 en algún tiempo futuro:
en algún tiempo futuro:
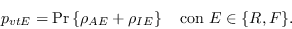 |
(35) |
Como es usual en modelos probabilistas, supondremos que 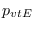 tiene una función de densidad exponencial,
tiene una función de densidad exponencial,
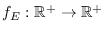 ,
,
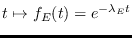 , donde
, donde
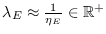 es el inverso multiplicativo del número esperado
es el inverso multiplicativo del número esperado
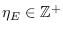 de individuos que “pasan” la epidemia recuperándose, si
de individuos que “pasan” la epidemia recuperándose, si 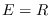 , o falleciendo, si
, o falleciendo, si 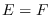 .
.
Por otro lado, para cada tiempo
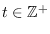 , sea
, sea
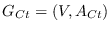 la gráfica dirigida cuyos nodos son los individuos y
la gráfica dirigida cuyos nodos son los individuos y
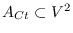 consta de las parejas ordenadas
consta de las parejas ordenadas 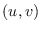 tales que
tales que 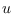 ha contagiado a
ha contagiado a 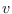 antes o en el tiempo
antes o en el tiempo 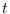 . Para cada
. Para cada 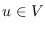 tal que
tal que
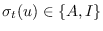 , sea
, sea 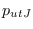 la probabilidad de que el individuo
la probabilidad de que el individuo 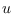 , asintomático o infeccioso, contagie a uno susceptible. Naturalmente, se ha de tener:
, asintomático o infeccioso, contagie a uno susceptible. Naturalmente, se ha de tener:
![\begin{displaymath}
\forall v\in V:\ \left[\sigma_t(s)=S\ \Longrightarrow\ p_{vt...
...n\mbox{\rm Vec}(v)\land\sigma_t(u)\in \{A,I\}\right\}\right].
\end{displaymath}](img280.png) |
(36) |
Con fines de simplificar la modelación, supongamos que es uniforme y no depende del tiempo la probabilidad de que un contagiado contagie a alguien que no lo sea, es decir
Entonces la condición (36) queda
![\begin{displaymath}
\forall v\in V:\ \left[\sigma_t(s)=S\ \Longrightarrow\ p_{vt...
...eft(\mbox{\rm Vec}(v)\cap \sigma_t^{-1}\{A,I\}\right)\right].
\end{displaymath}](img282.png) |
(37) |
Si
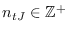 es el valor esperado del número de contagiados en contacto directo con un individuo susceptible, es decir
es el valor esperado del número de contagiados en contacto directo con un individuo susceptible, es decir
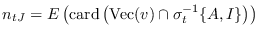 entonces la condición (37) queda
entonces la condición (37) queda
![\begin{displaymath}
\forall v\in V:\ \left[\sigma_t(s)=S\ \Longrightarrow\ p_{vtSA} + p_{vtSI} = p_Jn_{tJ}\right].
\end{displaymath}](img285.png) |
(38) |
Pues bien, se tiene:
Por otro lado,
![\begin{displaymath}
\forall v\in V:\ \left[\sigma_t(s)=S\ \Longrightarrow\ p_{vtSS} \approx (1-p_J)^{n_{tJ}}\right],
\end{displaymath}](img291.png) |
(41) |
Así pues,
lo cual establece condiciones entre 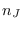 y
y 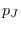 .
.
Considérese pues la aplicación polinómica respecto a 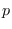 , pero exponencial respecto a
, pero exponencial respecto a 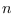 :
:
Se tiene que para toda 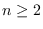 ,
, 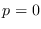 es una raíz de multiplicidad 2 del polinomio
es una raíz de multiplicidad 2 del polinomio 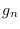 , sin embargo, ya que el primer sumando de
, sin embargo, ya que el primer sumando de 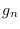 tiende a 0 en
tiende a 0 en ![$]0,1]$](img300.png) más rápido que el resto cuando
más rápido que el resto cuando 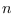 aumenta de tamaño, habrá una raíz de
aumenta de tamaño, habrá una raíz de 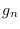 distinta de cero en
distinta de cero en ![$]0,1]$](img300.png) y ha de tenerse
y ha de tenerse 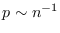 .
.
![]() el conjunto de individuos en una localidad donde se desarrolla una epidemia. En todo momento, se tiene una partición de
el conjunto de individuos en una localidad donde se desarrolla una epidemia. En todo momento, se tiene una partición de ![]() en las clases siguientes:
en las clases siguientes:
![]() donde los nodos son los individuos y
donde los nodos son los individuos y
![]() consta de las aristas consistentes de parejas de individuos con cercanía geográfica, familiares o de trabajo. La distancia entre dos nodos es el número de aristas de las que consta el camino más corto que los une en la gráfica, adirigida,
consta de las aristas consistentes de parejas de individuos con cercanía geográfica, familiares o de trabajo. La distancia entre dos nodos es el número de aristas de las que consta el camino más corto que los une en la gráfica, adirigida, ![]() .
Para cada
.
Para cada ![]() sea
sea
![]() la vecindad de
la vecindad de ![]() en esa gráfica de contactos, es decir un nodo
en esa gráfica de contactos, es decir un nodo ![]() es vecino de
es vecino de ![]() si está a distancia 1 de
si está a distancia 1 de ![]() .
.
![]() el conjunto de estados que puede asumir cada nodo, o de clases en la que están los nodos.
En cada momento
el conjunto de estados que puede asumir cada nodo, o de clases en la que están los nodos.
En cada momento ![]() se tiene una función de asignación:
se tiene una función de asignación:
![]() que a cada nodo le asocia un estado en el tiempo
que a cada nodo le asocia un estado en el tiempo ![]() . Se dice que el individuo
. Se dice que el individuo ![]() “es”
“es” ![]() al momento
al momento ![]() .
.
![]() , cada nodo
, cada nodo ![]() , para todos
, para todos ![]() sea
sea
![\begin{displaymath}P_{vt} = \left[\begin{array}{ccccc}
p_{vtSS} & p_{vtSA} & p_...
...
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1
\end{array}\right].\end{displaymath}](img243.png)
![]() se muestra en la Figura 2. Las probabilidades en la diagonal son las de quedarse en un mismo estado. Para todos
se muestra en la Figura 2. Las probabilidades en la diagonal son las de quedarse en un mismo estado. Para todos ![]() denotemos por
denotemos por
![]() a la transición que va de
a la transición que va de ![]() a
a ![]() mismo y por
mismo y por
![]() a la que va del estado
a la que va del estado ![]() al
al ![]() . Así, toda ruta para ir de
. Así, toda ruta para ir de ![]() a cualquiera de los estados finales se expresa mediante la expresión regular
a cualquiera de los estados finales se expresa mediante la expresión regular
![]() es
es
![\begin{eqnarray*}
\left[\sum_{\iota=0}^{+\infty}p_{vtSS}^{\iota}\right]p_{vtSA}\...
...{p_{vtSA}}{p_{vtSA}+p_{vtSI}}\frac{p_{vtAR}}{p_{vtAR}+p_{vtAI}}.
\end{eqnarray*}](img262.png)
![]() , sea
, sea
![]() la gráfica dirigida cuyos nodos son los individuos y
la gráfica dirigida cuyos nodos son los individuos y
![]() consta de las parejas ordenadas
consta de las parejas ordenadas ![]() tales que
tales que ![]() ha contagiado a
ha contagiado a ![]() antes o en el tiempo
antes o en el tiempo ![]() . Para cada
. Para cada ![]() tal que
tal que
![]() , sea
, sea ![]() la probabilidad de que el individuo
la probabilidad de que el individuo ![]() , asintomático o infeccioso, contagie a uno susceptible. Naturalmente, se ha de tener:
, asintomático o infeccioso, contagie a uno susceptible. Naturalmente, se ha de tener:
![]() , pero exponencial respecto a
, pero exponencial respecto a ![]() :
: