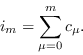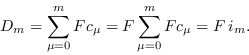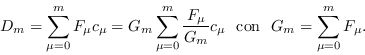Next: Modelo de Richards Up: Modelos simplificados Previous: Modelos simplificados Contents
Sea ![]() el número básico de reproducción que puede pensarse como el número de individuos susceptibles contagiados por uno infeccioso.
Sea
el número básico de reproducción que puede pensarse como el número de individuos susceptibles contagiados por uno infeccioso.
Sea ![]() el tiempo de incubación.
el tiempo de incubación.
Si se supone ![]() constante, al tiempo
constante, al tiempo
![]() el número de contagiados habrá aumentado en un factor
el número de contagiados habrá aumentado en un factor
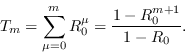
Si ![]() varía con el tiempo, digamos
varía con el tiempo, digamos ![]() es el número básico de reproducción vigente en el período
es el número básico de reproducción vigente en el período ![]() -ésimo, o sea
-ésimo, o sea
![]() siendo
siendo ![]() , el factor de crecimiento será
, el factor de crecimiento será
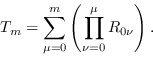
Si ![]() es el número de nuevos casos infectados en, entonces el número total de infecciosos a lo largo de la pandemia será
es el número de nuevos casos infectados en, entonces el número total de infecciosos a lo largo de la pandemia será