Modelo de Richards

Este modelo se presenta en [5]. Utilizaremos la notación en la sección 1.1. Sea $t\mapsto I(t)$ una medida de los infecciosos y sea $F:\mathbb{R}^+\to\mathbb{R}^+$ una función determinada por las decisiones de control de la epidemia. Se ha de tener

$$\frac{d I}{dt}(t) = r \frac{I}{F\circ I}(t)\ \mbox{ con }\ r... ...ta}}\ln R_0\in\mathbb{R}^+\ \mbox{ y }\ R_0 = e^{rt_{\iota}},$$ (1)

y,

$$F_{N_0a}:n\mapsto\left(1-\left(\frac{n}{N_0}\right)^a\right)^{-1} = \frac{N_0^a}{N_0^a-n^a}\ \mbox{ con }\ a\in\mathbb{R}^+.$$

En la Figura 1 se bosqueja algunas de estas funciones para diversos exponentes $a$. Como se ve, $F_{N_0a}(0)=1$ y en $n=N_0$, $F_{N_0a}$ tiene un polo, una singularidad. Naturalmente el dominio de interés es $[0,N_0[$. Se tiene:

$$\frac{dF_{N_0a}}{dn}(n) = N_0^aa\frac{1}{(N_0^a-n^a)^2}\frac{... ..._0^aa\frac{n^a(1+a)-N_0^a(1-a)}{(N_0^a-n^a)^3}\frac{1}{n^{a+2}}$$

así pues, la segunda derivada se anula en el punto $N_a\in\mathbb{R}$ tal que $N_a^a =N_0^a \frac{1-a}{1+a}$ y se tendrá $N_a>0$ toda vez que $a\in]0,1[$.

Figure: Gráficas de las funciones $F_{N_0a}$, con $N_0=10$ en el intervalo $[0,N_0-N_0^{-1}]$. De izquierda a derecha se muestran las correspondientes a $a=\frac{1}{10},1,2,5$ respectivamente.

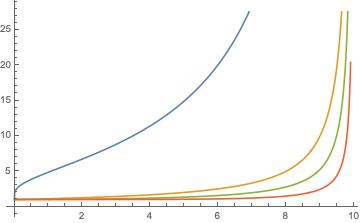En consecuencia, si $0<a<1$, $F_{N_0a}$ es cóncava en el intervalo $[0,N_a]$, en $N_a$ tiene un “punto silla”, es convexa de $]N_a,N_0[$ y tiende a infinito cuando $n\nearrow N_0$.

Por otro lado $F_{N_0a}\mathop{\longrightarrow}_{a\nearrow +\infty} 1$ puntualmente en $[0,N_0[$.

Las soluciones de (1) son de la forma

$$t\mapsto S_{rt_r}(t) =N_0\left[1 + e^{-r(t-t_r)}\right]^{-\fr... ... = \frac{1}{r}\ln\left[\left[\frac{N_0}{S_0}\right]^a-1\right].$$

Se considera la epidemia extinta cuando a lo largo de 3 meses, es decir, de 90 días, no aparezca caso alguno de infección, lo que ha de ocurrir en el tiempo

$$t_e = \mathop{\mbox{\rm arg min}}_{t_0}\left\{\int_{t_0}^{t_0+90}(N_0-S(t))\,dt<1\right\}.$$