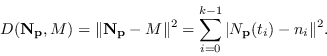La población de una cierta comunidad varía con el tiempo como
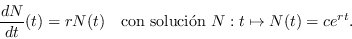 |
(2) |
donde
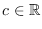 es una constante de integración.
En tiempo discreto,
es una constante de integración.
En tiempo discreto,
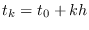 , con
, con 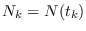 , por el Teorema del Valor Medio se tendrá
, por el Teorema del Valor Medio se tendrá
O sea
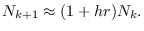 Para
Para
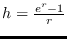 se tendrá, a grandes rasgos
se tendrá, a grandes rasgos
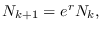 lo que refrenda que la solución tiene un crecimiento exponencial:
lo que refrenda que la solución tiene un crecimiento exponencial:
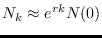 .
.
Otra modelación es la siguiente
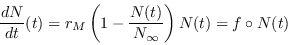 |
(3) |
donde 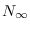 es el máximo de la población en el intervalo de tiempo considerado,
es el máximo de la población en el intervalo de tiempo considerado, 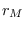 es proporcional a la tasa de variación de
es proporcional a la tasa de variación de 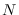 en ese punto y
en ese punto y
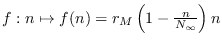 .
La solución típica de (3) es
.
La solución típica de (3) es
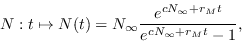 |
(4) |
donde 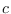 es una constante de integración. Puede verse que, en efecto, vale (3),
es una constante de integración. Puede verse que, en efecto, vale (3),
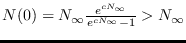 y
y 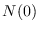 estará más cercano a
estará más cercano a 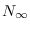 en tanto que
en tanto que 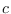 sea más grande, y
sea más grande, y
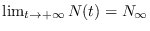 .
Las dos primeras derivadas de la solución son
.
Las dos primeras derivadas de la solución son
En tiempo discreto,
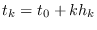 , con
, con 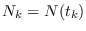 . Tomando pasos variables
. Tomando pasos variables
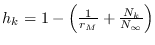 , se podría escribir
, se podría escribir
El comportamiento de las soluciones en (2) y (4) son disímiles. Denotemos por 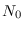 la solución en (2) y por
la solución en (2) y por 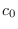 a su constante de integración, de igual manera denotemos por
a su constante de integración, de igual manera denotemos por 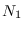 la solución en (2) y por
la solución en (2) y por 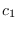 a su constante de integración. Consideremos la interpolación
a su constante de integración. Consideremos la interpolación
![\begin{displaymath}
N_p:t\mapsto (1-p)N_0(t) + pN_1(t) = \frac{e^{r t} }{e^{c_1 ...
...y}} - c_0 (1-p)\left[1 - e^{c_1 N_{\infty}+r t}\right]\right)
\end{displaymath}](img71.png) |
(5) |
cuya derivada es
En el punto inicial, 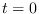 se tiene
se tiene
y este valor, por lo general, será no-negativo, a menos que 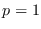 . Esto significa que inicialmente
. Esto significa que inicialmente 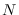 es creciente, en las raices de
es creciente, en las raices de 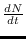 tendrá valores extremos y posteriormente,
tendrá valores extremos y posteriormente,
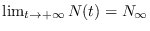 .
.
La función 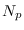 dada depende de los parámetros
dada depende de los parámetros
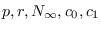 por lo que se debería escribir
por lo que se debería escribir
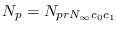 .
Así pues, dada una muestra de valores
.
Así pues, dada una muestra de valores
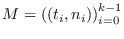 , donde se quiere que
, donde se quiere que
![$\forall i\in[\![0,k-1]\!]$](img81.png) :
:
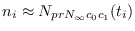 se ha de localizar los parámetros
se ha de localizar los parámetros
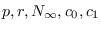 mediante cuadrados mínimos.
mediante cuadrados mínimos.
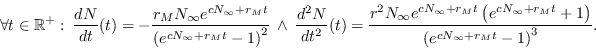
![]() dada depende de los parámetros
dada depende de los parámetros
![]() por lo que se debería escribir
por lo que se debería escribir
![]() .
Así pues, dada una muestra de valores
.
Así pues, dada una muestra de valores
![]() , donde se quiere que
, donde se quiere que
![]() :
:
![]() se ha de localizar los parámetros
se ha de localizar los parámetros
![]() mediante cuadrados mínimos.
mediante cuadrados mínimos.