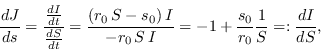Modelo SIR

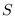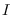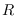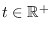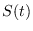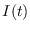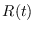En todo momento, la población se divide en tres clases: $S$, consistente de los individuos susceptibles, $I$, consistente de los individuos infecciosos y $R$, consistente de los individuos recuperados. En cada instante $t\in\mathbb{R}^+$, $S(t)$, $I(t)$ y $R(t)$ denotan los números de individuos de esos tipos, respectivamente, o con fines de asociarles valores reales, de medidas.

El modelo SIR queda establecido por las ecuaciones

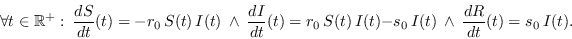$$\forall t\in\mathbb{R}^+:\ \frac{d S}{dt}(t) = - r_0\,S(t)\,... ...\,I(t) - s_0\,I(t)\ \ \land\ \ \frac{d R}{dt}(t) = s_0\,I(t).$$ (6)

A grandes rasgos, si 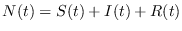$N(t) = S(t) + I(t) + R(t)$ es la población total, 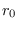$r_0$ es la tasa de individuos contagiados por uno ya contagiado y 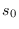$s_0$ es la proporción de recuperados entre los infecciosos, entonces

• el decremento de los susceptibles de contagio varía como $r_0N(t)\,\frac{S(t)}{N(t)}\,I(t) = r_0\,S(t)\,I(t),$
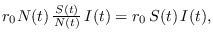
• el incremento de los recuperados varía como $s_0\,I(t).$
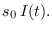
• el incremento de los infecciosos varía según se incrementen los susceptibles o se decrementen los recuperados.

Sea 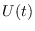$U(t)$ la medida (o número) de los individuos que se mantienen como infectuosos habiendolo sido previamente. Entonces 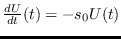$\frac{d U}{dt}(t) = -s_0U(t)$ por lo que, necesariamente 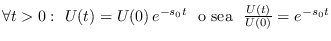$\forall t>0:\ U(t) = U(0)\,e^{-s_0t}\ \mbox{ o sea }\ \frac{U(t)}{U(0)} = e^{-s_0t}$ lo que determina una densidad de probabilidad con media 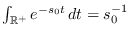$\int_{\mathbb{R}^+} e^{-s_0t}\,dt = s_0^{-1}$ y éste es el tiempo esperado de duración de la epidemia.

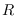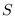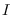En el sistema de ecuaciones (6), $R$ queda determinado por $S$ e $I$, así basta considerar el sistema

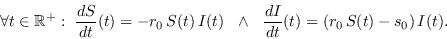$$\forall t\in\mathbb{R}^+:\ \frac{d S}{dt}(t) = - r_0\,S(t)\,I(t)\ \ \land\ \ \frac{d I}{dt}(t) = (r_0\,S(t) - s_0)\,I(t).$$ (7)

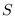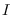Naturalmente, $S$ e $I$ no pueden ser negativas así que cuando asumen el valor 0 se puede considerar que se arriba a condiciones extremas del sistema (7). Para esto, el valor

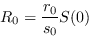$$R_0 = \frac{r_0}{s_0}S(0)$$ (8)

llamado básico de reproducción, es esencial para determinar el desempeño del sistema: Si 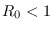$R_0<1$ la infección desaparece, en tanto que si 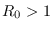$R_0>1$ surge una epidemia.

Ahora, supongamos que la medida de los infecciosos se pone en función de la de los susceptibles, sea 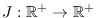$J:\mathbb{R}^+\to\mathbb{R}^+$ tal función. Entonces, se ha de tener 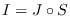$I = J\circ S$. Expresado esto en diagramas, queda

$$\begin{array}{cc} \xymatrix{ \mathbb{R}^+ \ar[r]^{S} \ar[rd... ...\ & i\in\{\mbox{ infecciosos }\}% } \\ (a) & (b) \end{array}$$ (9)

Por la Regla de la Cadena se ha de tener 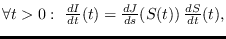$\forall t>0:\ \frac{d I}{dt}(t) = \frac{dJ}{ds}(S(t))\,\frac{d S}{dt}(t),$ o escrito de manera abreviada

$$\frac{dJ}{ds} = \frac{ \frac{dI}{dt} }{ \frac{dS}{dt} } = \f... ...\,S\,I } = -1 + \frac{s_0}{r_0} \frac{1}{S} =: \frac{dI}{dS},$$

de donde, al calcular una antiderivada, se ha de tener que, para una constante de integración $c\in\mathbb{R}$:

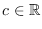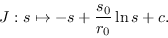$$J: s\mapsto -s +\frac{s_0}{r_0}\ln s + c.$$ (10)

Resulta,

$$\forall s\in\mathbb{R}^+:\ \frac{dJ}{ds} = \frac{s_0}{r_0}\frac{1}{s}-1,$$

y esa derivada asumirá el valor 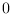$0$ en el punto 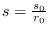$s=\frac{s_0}{r_0}$. Para éste se tendrá:

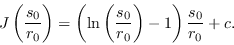$$J\left(\frac{s_0}{r_0}\right) = \left(\ln\left(\frac{s_0}{r_0}\right)-1\right)\frac{s_0}{r_0} + c.$$ (11)

De la relación (10) se puede definir

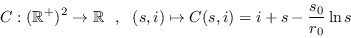$$C:(\mathbb{R}^+)^2\to\mathbb{R}\ \ ,\ \ (s,i)\mapsto C(s,i) = i + s -\frac{s_0}{r_0}\ln s$$ (12)

cuyas curvas de nivel, o contornos, corresponderán a los lugares geométricos correspondientes a parejas 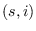$(s,i)$ que satisfacen el sistema (7). Se observa que se cumplen las propiedades siguientes:

• Para las condiciones iniciales 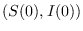$(S(0),I(0))$, el correspondiente contorno estará a la altura dada por la relación (12), a saber $c_0 = C(S(0),I(0))$.
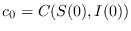• En cada contorno 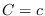$C=c$, el máximo valor que puede asumir 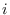$i$ se alcanza con 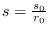$s=\frac{s_0}{r_0}$y este máximo está dado por (11).
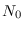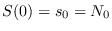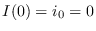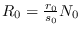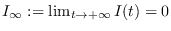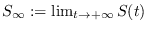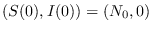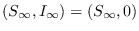• Si $N_0$ es la población inicial entonces $S(0) = s_0 = N_0$ e $I(0) = i_0 = 0$, con lo que, de acuerdo con (8), $R_0 = \frac{r_0}{s_0}N_0$. Bajo la suposición de que la infección fenecerá a la larga, se ha de tener $I_{\infty}:=\lim_{t\to+\infty}I(t) = 0$. Escribamos $S_{\infty}:=\lim_{t\to+\infty}S(t)$. Los puntos $(S(0),I(0)) = (N_0,0)$ y $(S_{\infty},I_{\infty}) = (S_{\infty},0)$ están en un mismo contorno, luego
  
  $$N_0-\frac{s_0}{r_0}\ln N_0 = C(S(0),I(0)) = C(S_{\infty},0) = S_{\infty}-\frac{s_0}{r_0}\ln S_{\infty}$$
  
  
  y en consecuencia
  
  $$\frac{r_0}{s_0} = \frac{\ln N_0 - \ln S_{\infty}}{N_0-S_{\infty}}$$
  
  
  lo que permite estimar la razón 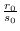$\frac{r_0}{s_0}$ en términos de los observables 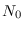$N_0$ y $S_{\infty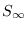}$. También se ha de tener
  
  $$R_0 = \frac{\ln N_0 - \ln S_{\infty}}{N_0-S_{\infty}}N_0 = \frac{\ln N_0 - \ln S_{\infty}}{1-\frac{S_{\infty}}{N_0}}.$$
  
  
  Sin embargo estos últimos estimativos sólo pueden obtenerse a porteriori. Son útiles pues para realizar tareas de diagnóstico o explicación, mas no de pronóstico.
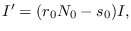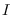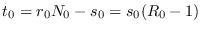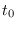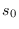• Ahora bien, la segunda ecuación en (7) puede aproximarse como $I' = (r_0N_0 - s_0)I,$ por lo que la tasa de inicial de crecimiento de $I$ es $t_0=r_0N_0 - s_0 = s_0(R_0-1)$. Así que, si $t_0$ y $s_0$ son estimados experimentalmente al inicio de la epidemia, se habrá de tener
  
  $$r_0 = \frac{1}{N_0}(t_0-s_0)\ \ \land\ \ R_0 = \frac{t_0}{s_0} - 1.$$