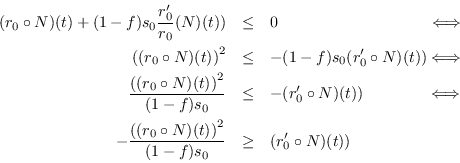Modelo con tasa general de contacto
En las ecuaciones (7), en vez de que 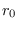 sea constante, se le supone como una función de la población actual:
sea constante, se le supone como una función de la población actual:
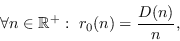 |
(13) |
donde
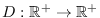 es no-decreciente.
Bajo la suposición de que la tasa de contactos ha de saturarse, se impone la condición
es no-decreciente.
Bajo la suposición de que la tasa de contactos ha de saturarse, se impone la condición
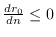 , la cual impone a su vez
, la cual impone a su vez
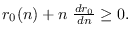
En algunos modelos, 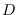 se considera de las formas siguientes
se considera de las formas siguientes
para algunas constantes
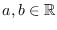 adecuadas (en la tercera función,
adecuadas (en la tercera función, 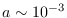 ).
).
Supongamos que de la población que deja de estar entre los infecciosos, una fracción 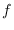 es debido a que se recupera y la proporción complementaria
es debido a que se recupera y la proporción complementaria 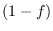 lo hace por fallecimiento. Denotemos por
lo hace por fallecimiento. Denotemos por
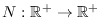 a la función que describe la población total actual. Se tiene entonces el sistema de ecuaciones
a la función que describe la población total actual. Se tiene entonces el sistema de ecuaciones
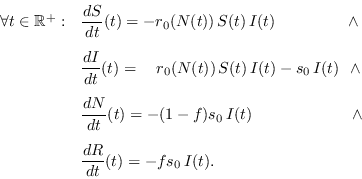 |
(14) |
y también en este caso, la última está determinada por las tres primeras. El número básico de reproducción es
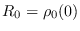 , donde
, donde
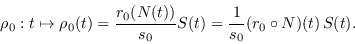 |
(15) |
La epidemia ha de fenecer si a la larga 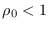 . Derivando (15) se ha de tener
. Derivando (15) se ha de tener
y esta derivada será no-negativa sólo cuando
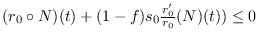 . Ahora
. Ahora
Así pues, a menos que 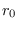 tuviese una derivada “muy negativa”, es decir, decreciera a gran ritmo, o sea que los susceptibles pasarían con mayor rapidez a la clase de los infeccciosos, la función
tuviese una derivada “muy negativa”, es decir, decreciera a gran ritmo, o sea que los susceptibles pasarían con mayor rapidez a la clase de los infeccciosos, la función 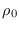 ha de ser no-creciente.
ha de ser no-creciente.
Por otro lado, de (14), se tiene
y al integrar
Al inicio, 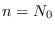 es la población cuando comienza la infección, a la larga
es la población cuando comienza la infección, a la larga 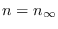 es la población restante cuando la epidemia fenece.
Puesto que
es la población restante cuando la epidemia fenece.
Puesto que
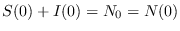 se ha de tener
se ha de tener
Haciendo
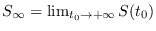 y suponiendo que
y suponiendo que 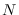 es decreciente así como
es decreciente así como
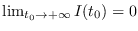 (es decir, la epidemia fenece),
(es decir, la epidemia fenece),
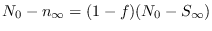 o sea
o sea
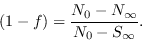 |
(16) |
![]() sea constante, se le supone como una función de la población actual:
sea constante, se le supone como una función de la población actual:
![]() se considera de las formas siguientes
se considera de las formas siguientes
![]() es debido a que se recupera y la proporción complementaria
es debido a que se recupera y la proporción complementaria ![]() lo hace por fallecimiento. Denotemos por
lo hace por fallecimiento. Denotemos por
![]() a la función que describe la población total actual. Se tiene entonces el sistema de ecuaciones
a la función que describe la población total actual. Se tiene entonces el sistema de ecuaciones
![\begin{eqnarray*}
\frac{d \rho_0}{dt}(t) &=& \frac{1}{s_0}\left[(r_0\circ N)(t)\...
...left[(r_0\circ N)(t) + (1-f)s_0
\frac{r_0'}{r_0}(N)(t))\right]
\end{eqnarray*}](img158.png)