La Teoría Musical ha tenido diversos acercamientos con las Matemáticas, y acaso de las seis Bellas Artes Clásicas, a saber, arquitectura, escultura, pintura, música, declamación y danza, la música es la que se ha tratado más con métodos matemáticos, aún desde los tiempos de Pitágoras de Samos. En la segunda mitad del S. XIX, Hugo Riemann (1849-1919) propuso una serie de transformaciones entre notas y acordes y la composición de ellas las estudió desde el punto de vista de la Teoría de Grupos.
Presentamos aquí, sin pretensión alguna de originalidad, diversos formalismos que permiten el análisis de composiciones musicales como estructuras algebraicas, como productos de gramáticas formales y como productos de procesos estocásticos.
Inicialmente, presentamos las operaciones riemannianas siguiendo un enfoque convencional introducido en [2] y que se ha utilizado en diversos análisis de música popular [1]. Recordamos la noción de tríadas y sus diversas connotaciones, tanto como acordes que como transformaciones. Buscamos ser precisos en distinguir esas dos connotaciones, lo que es muy común pasar por alto en textos de Teoría Musical. Después presentamos las acciones de grupos simétricos y de otros semigrupos sobre las tríadas. Pasamos luego a considerar los órdenes de tonos y operaciones para generar unos a partir de otros. Aquí ponemos especial cuidado en calcular cuántas tales transformaciones existen.
Finalmente, a manera de aplicaciones en Composición Musical recordamos laconstrucción de gráficas de tonos, etiquetadas por operaciones entre tríadas, y describimos las trayectorias como palabras resultantes de gramáticas regulares, esto en línea con tratados más extensos de composición musical basada en gramáticas formales [3,4]. También, vistas las trayectorias como paseos aleatorios, describimos someramente la noción de procesos markovianos, enfoque muy usual en la actualidad en la composición musical de tipo automático [5].
En la música occidental, 12 semitonos componen la escala
dodecafónica o cromática, de ellos 7 son diatónicos:
do, re, mi, fa, sol, la, si, y 5 cromáticos: do#,
re#, fa#, sol#, la#, y puestos en forma ascendente
quedan: do, do#, re, re#, mi, fa, fa#, sol, sol#, la, la#, si.
Se les pone en correspondencia con los elementos de
![]() . En
símbolos, si
. En
símbolos, si
![]() es un grupo
abeliano con la estructura de suma directa de sus factores, y es
de orden
es un grupo
abeliano con la estructura de suma directa de sus factores, y es
de orden
![]() .
.
Si un semitono ![]() se
toma como una raíz, se establece que
se
toma como una raíz, se establece que
Ahora bien, las operaciones riemannianas son las
siguientes:
Cada aplicación
![]() determina una aplicación entre tríadas
determina una aplicación entre tríadas
![]() ,
haciendo
,
haciendo
![]() :
:
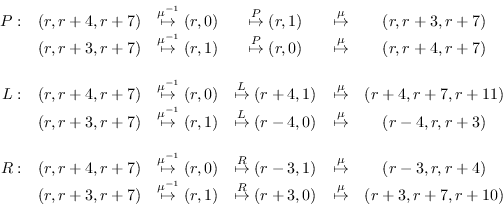
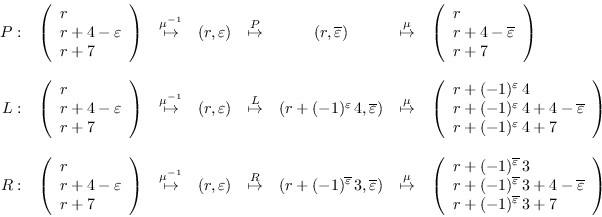

De manera alternativa y más convencional se tiene la de las transformaciones
uniformes de tríadas (uniform triadic transformations
(UTT)) presentada en [2]. Tales
UTT son las siguientes:
De las relaciones (3)-(5) resulta ![]() ,
,
![]() y
y
![]() .
.
La colección de aplicaciones
Por tanto cada permutación
![]() tiene
como orden en el grupo simétrico
tiene
como orden en el grupo simétrico ![]() a un divisor de 24.
a un divisor de 24.
Por otro lado, al escribir a los puntos en
![]() como
como
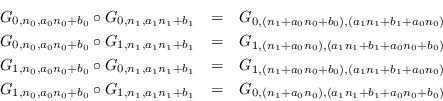
![\begin{eqnarray*}
m_1 &=& m_0 + (a_1n_1+a_0n_0+b_1+\delta_1b_0) -
(n_1+a_0n_0 +(...
...\
&=& m_0 +
\left[(a_1-1)n_1+b_1+(1-2(1-\delta_1))b_0\right] .
\end{eqnarray*}](img94.png)
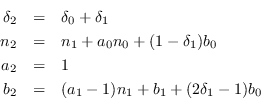
Observamos que al fijar
![]() , la ecuación
, la ecuación ![]() tiene 12
soluciones en
tiene 12
soluciones en
![]() cuando
cuando ![]() y son
de la forma
y son
de la forma ![]() ,
con
,
con
![]() ; mas cuando
; mas cuando ![]() hay soluciones si
y sólo si
hay soluciones si
y sólo si
![]() y en tal caso para cada tal
y en tal caso para cada tal
![]() hay
hay
![]() correspondientes
correspondientes
![]() . En suma, la
ecuación
. En suma, la
ecuación ![]() posee
posee
![]() soluciones
soluciones ![]() para cada
para cada
![]() . Ahora, observamos también
. Ahora, observamos también
De acuerdo con la Observación 2.4, cada
permutación
![]() tiene
un orden que es un divisor de
tiene
un orden que es un divisor de ![]() . Puede verse que hay 48
funciones de la forma
. Puede verse que hay 48
funciones de la forma
![]() ,
diferentes a pares, que dan permutaciones de orden 24 y todas
ellas corresponden a tomar
,
diferentes a pares, que dan permutaciones de orden 24 y todas
ellas corresponden a tomar ![]() . Una lista exhaustiva de
ellas, con repeticiones, se sintetiza con las reglas siguientes:
. Una lista exhaustiva de
ellas, con repeticiones, se sintetiza con las reglas siguientes:
Para una tríada de semitonos
![]() , su tríada de diferencias es
, su tríada de diferencias es
![]() . Así pues para
toda tríada mayor
. Así pues para
toda tríada mayor ![]() se tiene
se tiene
![]() en tanto que para toda tríada menor
en tanto que para toda tríada menor ![]() se tiene
se tiene
![]() .
.
Se representa a ![]() (el grupo de permutaciones de tres elementos) mediante las
permutaciones de la lista
(el grupo de permutaciones de tres elementos) mediante las
permutaciones de la lista ![]() :
:
![\begin{eqnarray*}
S_3 &=& \left[\,[3, 4, 5], [4, 5, 3], [5, 3, 4], [4, 3,
5], [3...
...a_0, \sigma_1,\sigma_2,\sigma_3,\sigma_4,\sigma_5\,\right].
%\\
\end{eqnarray*}](img137.png)
Consideremos el conjunto de semitonos ![]() definido por la
relación (1).
En el ambiente musical, una permutación de
definido por la
relación (1).
En el ambiente musical, una permutación de ![]() se llama un orden de
tonos (en inglés tone row y en alemán Tonreihe).
En esta presentación usaremos “permutación” de
se llama un orden de
tonos (en inglés tone row y en alemán Tonreihe).
En esta presentación usaremos “permutación” de ![]() y dejaremos de lado el
acuerdo musical “orden”. Si se tiene una permutación, digamos
y dejaremos de lado el
acuerdo musical “orden”. Si se tiene una permutación, digamos
![]() , se la divide de tres en tres y se escribe
, se la divide de tres en tres y se escribe
![\begin{eqnarray*}
\left[\begin{array}{c} t_0 \\ t_1 \\ t_2 \end{array}\right]
&\...
...silon_0-4)\\ t_1 \\ t_2+r +(7\varepsilon_0-4)
\end{array}\right]
\end{eqnarray*}](img164.png)
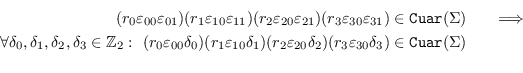
Igualmente, si ![]() es una tríada,
es una tríada,
![]() es un
múltiplo de
es un
múltiplo de ![]() .
.
Dada una tríada ![]() se tiene la relación siguiente en
se tiene la relación siguiente en
![]() :
:
se define
si al escribir, como en (15),
![\begin{displaymath}\psi_{\rho_0}(\tau)
= \left[\begin{array}{c} \tau_{00} \\ \ta...
...u_{01} \\ \tau_{11} \\ \tau_{21} \\
\tau_{31}\end{array}\right]\end{displaymath}](img204.png)
se ha de tener que la tríadaEntoncescoincide con
o bien con
.
Ahora, recordemos las funciones
![]() definidas en (7). Para
definidas en (7). Para
![]() vale
vale
Si para una tríada ![]() se tiene
se tiene
![]() entonces existen transformaciones de la
forma
entonces existen transformaciones de la
forma
![]() tales
que vale el diagrama
tales
que vale el diagrama
![\begin{displaymath}\xymatrix{
(r_0\varepsilon_{00}) \ar@{\vert->}[d]_{G_{\delta_...
...->}[r]_{G_{\delta_4 s_{40}s_{41}}} &
(r_2\varepsilon_{20}) %
} \end{displaymath}](img219.png)
Mediante las operaciones riemannianas se define la gráfica
![]() donde
donde
![]() es
el conjunto de aristas dirigidas que consta de las
parejas ordenadas
es
el conjunto de aristas dirigidas que consta de las
parejas ordenadas
![]() tales que
tales que
Para dos elementos
![]() definimos
definimos
Podemos extender estas definiciones a todo el grupo ![]() definido
en (
definido
en (![[*]](crossref.png) ). Sea
). Sea ![]() la gráfica obtenida como
en (17), considerando
la gráfica obtenida como
en (17), considerando ![]() en vez de
en vez de ![]() solamente. Así se
ha de tener que
solamente. Así se
ha de tener que ![]() es una gráfica dirigida y como en (
es una gráfica dirigida y como en (![[*]](crossref.png) ) se define
) se define
![]() el
cual también es un lenguaje regular en
el
cual también es un lenguaje regular en ![]() . Similarmente, si
. Similarmente, si ![]() es un subgrupo de
es un subgrupo de
![]() se construye la
gráfica
se construye la
gráfica ![]() y para cualesquiera dos elementos
y para cualesquiera dos elementos
![]() el
lenguaje
el
lenguaje
![]() .
Observamos que siendo
.
Observamos que siendo ![]() y
y ![]() grupos, la
composición de dos funciones en ellos es un elemento en ellos. Por
tanto, cualquier trayectoria en
grupos, la
composición de dos funciones en ellos es un elemento en ellos. Por
tanto, cualquier trayectoria en
![]() puede ser sustituida por una sola arista, de
puede ser sustituida por una sola arista, de
![]() a
a
![]() .
.
La composición basada en gramáticas pretende generar gramáticas formales que caractericen a las trayectorias en las gráficas descritas que a su vez describan mejor temas pertenecientes a ciertos géneros musicales. Bien que aquí sólo nos hemos referido a gramáticas regulares, bien puede considerarse como alternativas algunas otras en la Jerarquía de Chomsky.
Sea
![]() un
conjunto no vacío. Mediante las correspondencias en el
diagrama (2),
un
conjunto no vacío. Mediante las correspondencias en el
diagrama (2), ![]() puede verse como un conjunto
de tríadas o como un conjunto de semitonos. Así,
puede verse como un conjunto
de tríadas o como un conjunto de semitonos. Así,
![]() , y sea
, y sea ![]() un conjunto de funciones
un conjunto de funciones ![]() . Para
fijar ideas, se podría tomar
. Para
fijar ideas, se podría tomar ![]() , como se vió en la
sección 2, y
, como se vió en la
sección 2, y ![]() el conjunto de operaciones
riemannianas. Sea
el conjunto de operaciones
riemannianas. Sea
![]() la correspondiente gráfica, según se definió en la sección 5. Para cada
la correspondiente gráfica, según se definió en la sección 5. Para cada ![]() sea
sea
![]() la vecindad de
la vecindad de ![]() en
en ![]() .
.
Un proceso markoviano en ![]() queda determinado por una
matriz
queda determinado por una
matriz
![]() donde
donde
Enumérese
![]() . Un paseo markoviano
es una sucesión
. Un paseo markoviano
es una sucesión
![]() tal
que
tal
que ![]() es una tríada inicial y
es una tríada inicial y
![]() ,
, ![]() resulta del proceso siguiente:
resulta del proceso siguiente:
Algunas variantes consisten en considerar la matriz ![]() dependiendo del
tiempo, dando lugar a series de tiempo, precisamente.
dependiendo del
tiempo, dando lugar a series de tiempo, precisamente.
Alternativamente, en vez de considerar probabilidades de transición entre tríadas, podría considerarse probabilidades sobre los propios paseos aleatorios generados, lo que da lugar a cadenas de Markov y variantes suyas.
De esta manera, se busca a caracterizar a los sistemas markovianos que ajustan mejor a alguna colección de temas musicales.