Se considera aquí a la clase de individuos que “potencialmente” son infecciosos pero son asintomáticos. Así, inicialmente
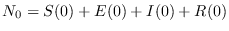 .
Se tiene ahora el sistema de ecuaciones
.
Se tiene ahora el sistema de ecuaciones
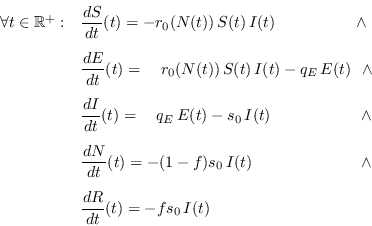 |
(17) |
y 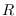 queda determinada por las primeras variables
queda determinada por las primeras variables 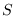 ,
, 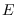 ,
, 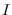 . Este modelo se trata de manera similar al visto en la sección 2.2 donde la vaiable
. Este modelo se trata de manera similar al visto en la sección 2.2 donde la vaiable 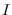 de ahí se sustituye por
de ahí se sustituye por 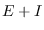 de este caso. Se ve pues que
de este caso. Se ve pues que 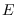 tiene poca relevancia.
tiene poca relevancia.
Supongamos ahora que una fracción de la población asintomática efectivamente transmite la infección. Digamos,
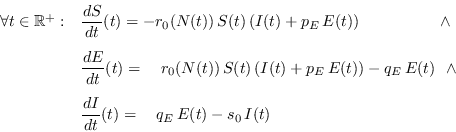 |
(18) |
En este caso se tendrá que el número básico de reproducción es
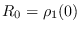 donde
donde
(t)\,N(t).
\end{displaymath}](img177.png) |
(19) |
Integrando las ecuaciones para
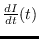 y
y
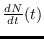 en (17) se obtiene
en (17) se obtiene
y de la primera ecuación en (18) se obtiene
suponiendo que 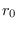 es decreciente y que
es decreciente y que
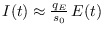 se ha de tener
se ha de tener
de donde se obtiene un estimativo del valor a la larga 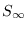 .
.
![]() .
Se tiene ahora el sistema de ecuaciones
.
Se tiene ahora el sistema de ecuaciones
![\begin{eqnarray*}
\log \frac{S(0)}{S_{\infty}} &\geq& r_0\circ N(0)\int_0^{+\inf...
...}E(t)\,dt \\
&=& R_0\left[-\frac{S_{\infty}}{N(0)} + 1\right]
\end{eqnarray*}](img186.png)